A circle is a set of all points in a plane which are equidistant from a fixed point in the plane. The fixed point is called the centre of the circle and distance from the centre to any pint on the circle is called the radius of the circle. There are many real world examples of circle are full moon, ring, wheel , coins , disc, etc. In the article, we discuss definition of circle , circumference of circle, area of the circle and different forms of equation of circle completely.
A
circle is a set of all points (locus) in a plane which are equidistant from a
fixed point in the plane, centre. A circle is a conic section. It is a slice of
a right cone parallel to the circular base of the cone.
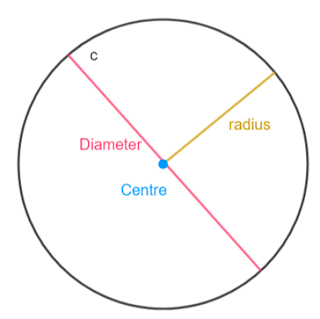
Terminology of a Circle
1) Centre : The fixed point equidistant from all points on the circle.
2) Radius : distance from the centre to any pint on the circle is called radius. The radius of circle is denoted by (r) or R.
3)
Diameter
: A line segment having
both the endpoints on the circle and passing through centre is called diameter
of circle. Diameter is the longest chord of the circle. Diameter of the circle
is twice the radius of the circle.
Diameter
is denoted by d.
Diameter , `r`
Radius , `r=\frac{d}{2}`
4)
Circumference
: The distance around the circle the circle or one revolution around the circle
is called circumference of the circle
(C).
Circumference of circle is given by
`C=2\pi r=\pi d`
5)
Area of the
circle : Total space occupied int the circle is called area of the circle (A).
Area
of the circle is given by
`A=\pi r^2`
In
terms of diameter,
`A=\frac{\pi d^2}{4}`
Equation of a Circle
There are
different forms of equation of a circle and all are interchanged by algebraic
manipulations in different forms.
Standard
form of a equation of a circle
In figure, C(h,k) is the centre and r is the radius of the circle. P(x,y) is any point on the circle.
`CP=r`
By distance formula,
` CP=\sqrt{(x-h)^2+(y-k)^2} `
`r=\sqrt{(x-h)^2+(y-k)^2}`
Squaring both sides,
`r^2=(x-h)^2+(y-k)^2`
`(x-h)^2+(y-k)^2=r^2`
This the standard form of a equation of circle. This is also called as the centre – radius form of equation of a circle.
Equation of a circle with centre at origin
Standard form of a equation of circle is given by
`(x-h)^2+(y-k)^2=r^2`
Since centre at origin (0,0), Put $h=0$ and $k=0$ in the above equation,
`(x-0)^2+(y-0)^2=r^2`
`x^2+y^2=r^2`
This is the equation of a circle with centre at origin.
Diameter form of Equation of Circle
In the figure, C is the centre of the circle. and `A(x_1,y_1)` and `B(x_2,y_2)` are the end points of the diameter of a circle. P(x,y) is any point the circle. Angle inscribed in a right angle; Hence ,`m\angle APB=90^\circ ` that is AP ⟂ BP
Slope of AP `=\frac{y-y_1}{x-x_1}` andSlope of BP`=\frac{y-y_2}{x-x_2}` ,
As AP ⟂ BP , product of their slopes is -1.
` \frac{y-y_1}{x-x_1}\times \frac{y-y_2}{x-x_2}=-1`
`(y-y_1)(y-y_2)=-(x-x_1)(x-x_2)`
`(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0`
This is called
the diameter form of equation of circle, where and are the end points of diameter of the circle.
General Equation
of a circle
Standard form of a equation of circle is given by
`(x-h)^2+(y-k)^2=r^2`
If this is the
same as equation `x^2+y^2+2gx+2fy+c=0 ` , then comparing coefficients,
`2g=-2h, 2f=-2k , c=h^2+k^2-r^2`
`∴(h,k)=(-g,-f) ` is the centre and
`r^2=h^2+k^2-c `
`r=\sqrt{g^2+f^2-c}` is the radius.
The general Equation of a circle is
`x^2+y^2+2gx+2fy+c=0`
Whose centre is `(-g,-f) ` and radius is `r=\sqrt{g^2+f^2-c}`
Parametric Form
of a Circle
Let P(x,y) be any
point on a circle with centre at O and radius r. As shown in figure , OP makes
an angle `\theta` with the positive direction of X-axis.
Draw PM ⟂ X - axis from P.
`\triangle OMP ` is a right – angled triangle.
`\cos{\theta}=\frac{OM}{OP}=\frac{x}{r}, \sin{\theta} =\frac{PM}{OP}=\frac{y}{r}`
`x=r\cos{\theta}, y=r\sin{\theta}`
This is the parametric form of the circle `x^2+y^2=r^2`
Note: The parametric form of circle is given by :`(x-h)^2+(y-k)^2=r^2`
`x=h+r\cos{\theta}, y=k+r\sin{\theta}`
Equation of
tangent to the Circle
Given equation of the circle is `x-^2+y^2=r^2` . The centre of the circle is at origin(0,0) and radius r.
Let `P(x_1,y_1)` be any point on the circle.
Slope of the OP `=\frac{y_1-0}{x_1-0}=\frac{y_1}{x_1}`
As a tangent
drawn to the circle at point P. Since OP is perpendicular to the tangent at
point P.
Slope of the
tangent,
`m=\frac{-x_1}{y_1}`
Equation of
tangent in slop-point form,
`y-y_1=\frac{-x_1}{y_1}(x-x_1)`
`y y_1-y_1^2=- x x_1+x_1^2`
`x x_1+yy_1=x_1^2+y_1^2 (a)`
As `(x_1,y_1)` lies on the circle,
`{x_1}^2+{y_1}^2=r2`
Therefore
equation becomes (a) ,
`x x_1+yy_1=r^2`
In general, equation of a tangent to a circle`x^2+y^2=r^2` at point ` P(x_,y_1)` is
`x x_1+yy_1=r^2`
Note: Equation of a tangent to the circle `x^2+y^2+2gx+2fy+c=0` at `(x_1,y_1)` is
`x x_1+yy_1+g(x+x_1)+f(y+y_1)+c`
Frequently Asked
Questions – FAQ
1)
What is a circle?
A circle is a set of all points in a plane which are equidistant from a fixed point in the plane. The fixed point is called the centre of the circle and distance from the centre to any pint on the circle is called the radius of the circle
2)
What is the
general equation of a circle?
The general Equation of a circle is
`x^2+y^2+2gx+2fy+c=0`
Whose centre is `(-g,-f) ` and radius is `r=\sqrt{g^2+f^2-c}`
3)
What are the parts of a circle?
The parts of a circle are the radius, diameter, circumference, arc, chord, secant, tangent, sector and segment. A round plane figure whose boundary consists of points equidistant from a fixed point.
4)
What is
parametric equation of a circle?
The parametric form of circle is given by :`{(x-h)^2+(y-k)^2}=r^2`
`x=h+r\cos{\theta}, y=k+r\sin{\theta}`
5)
What is equation
of tangent of a circle?
In general, equation of a tangent to a circle `x^2+y^2=r^2` at point ` P(x_,y_1)` is
`x x_1+yy_1=r^2`
Equation of a tangent to the circle `x^2+y^2+2gx+2fy+c=0` at `(x_1,y_1)` is
`x x_1+yy_1+g(x+x_1)+f(y+y_1)+c=0`










0 Comments